Introduction

栈：都从栈的尾部进出，后进入的元素先弹出
单调栈：栈中的元素，以某个方向呈现单调性

应用

可以用于查找下标为 i的元素，左边/右边第一个大于/小于其的第一个元素

Question

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式
第一行包含整数 N，表示数列长度。

第二行包含 N 个整数，表示整数数列。

输出格式
共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围
1≤N≤105
1≤数列中元素≤109
输入样例：

5
3 4 2 7 5

输出样例：

-1 3 -1 2 2

Train of Thought

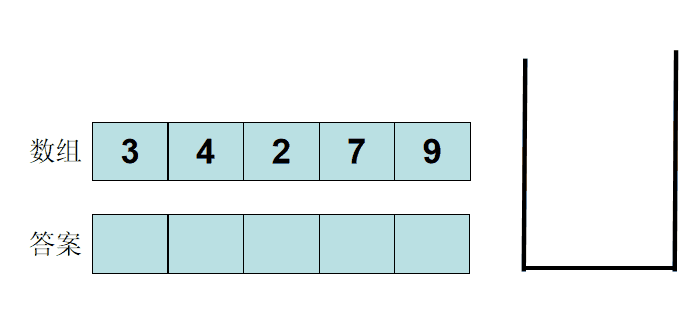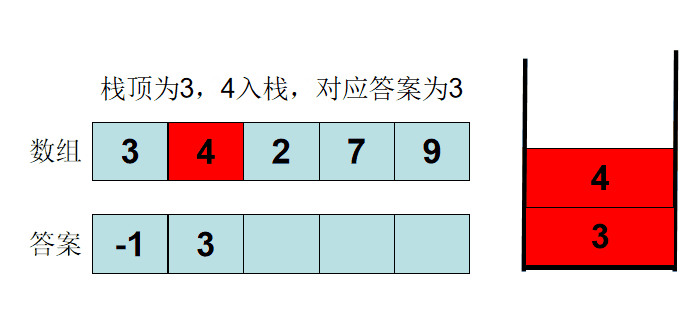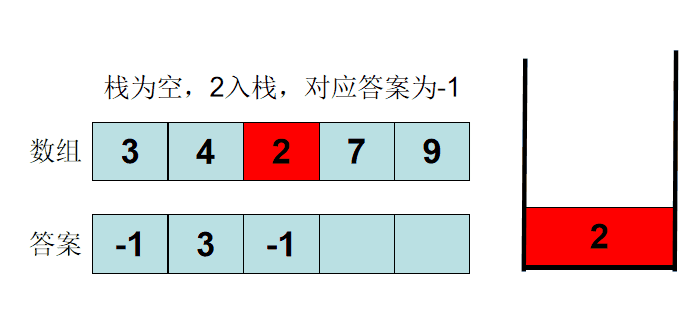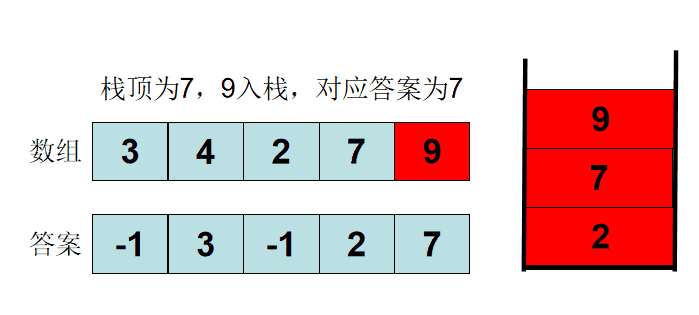
利用栈的特性，可以构造出一个单调栈：栈中存储的数，从栈头到栈尾，为单调递增。是所有可能成为答案的数

为什么是可能成为答案的数呢？进行分析：

读取一个数 x，与栈尾比较：

1. 如果 x大于栈尾，则栈尾就是 x左侧第一个小于它的数
2. 如果 x小于栈尾，则有两个结论：

• 栈尾不是答案，需要弹出栈尾，向前判断
• x比当前的栈尾还小，并且 x还排在栈尾后面，则：下一次寻找答案时，如果栈尾满足数值条件，那么 x一定也满足数值条件，所以 <u>栈尾再也不会成为答案 </u>

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 100010;
int stk[N], tt; // tt为栈尾，全局变量默认为0

int main () {
    int n;
    scanf("%d", &n);
  
    while (n -- ) {
        int x;
        scanf("%d", &x);
        while (tt && stk[tt] >= x ) tt --; // 栈尾弹出的条件：栈不空且栈尾大于x
        /*
            此时，
            要么栈元素全部弹出，stk变为空栈；
            要么栈尾已经小于x
        */
        if (!tt) printf("-1 "); // 判断是否空栈
        else printf("%d ", stk[tt]);
        stk[++ tt] = x; // 最后将x变成栈尾，实现了单调栈的维护更新
    }
    return 0;
}

清晰的图解：

Extraneous

Q：为什么单调栈不能令栈尾直接就是答案？
A：因为 x的数值不同，栈尾无法确保小于 x，不得不进行判断。
单调栈的本质组成其实是原数组中从前到后选取了部分元素，确保其满足单调

我们作为用户，在选取欲求数值时，既要从 x向左最近的，又要比 x小的。
这实际上是两种属性的竞争：靠 x位置越近，则优先级越高；比 x小，则能力强
<u>问题转化为：既要优先级高，又要能力强 </u>
由此才引发了竞争

反证：如果栈尾的元素在栈中最小，那么既满足了优先级最高，又满足了能力强。这就可以直接成为答案，还需要什么判断么？
同理，如果优先级差，能力还不强，那一定是没有可能成为答案的。

吉布斯自由能变 ΔG

反应能否自发，取决于两个因素：ΔH和温度
如果二者异号，则可以定性唯一确定 ΔG的符号；如果二者同号，才需定量计算 ΔG

那么人才市场呢？

倘若只需要招一名人才
如果年龄又小、能力又强、又肯感恩，那么毫无疑问可以是最佳选择；
如果没有较小的年龄、感恩意识又差、那么只能通过能力进行竞争了。